Algebraic Expressions Teaching Resources
Explore the world of algebraic expressions in math class this year with the help of Teach Starter! This collection of printable and digital math resources was created by teachers for teachers like you.
Teach students how to read expressions with letters standing in for numbers, explore the parts of an expression and more this school year with the help of activities and games aligned with both TEKS and the Common Core math curriculum. This resource collection includes everything you need to plan lessons for fifth, sixth and seventh grade algebra classes!
Is this your first year teaching upper elementary or middle school math? Looking for a handy guide? Read on for a primer from our teacher team!
What Is an Expression in Math? A Kid-Friendly Definition
The term expression has a very specific meaning in math, so it helps to clarify for your students what you mean when you say "expression." Here's a definition that you can use with students:
An expression is a math statement that's made up of numbers and operation symbols. It does not include an equal sign and can include variables.
What Is an Algebraic Expression? A Kid-Friendly Definition
So, if that's the definition of expression, what happens when you add the word "algebraic" at the front?
An algebraic expression is a math statement that's composed of numbers, operations and variables.
These are also sometimes called variable expressions.
How to Evaluate an Algebraic Expression
A core skill of working with algebraic expressions is evaluating these math statements.
Evaluating is how we find the value of the expression when a given number replaces the variable. So how does it work? Let's walk through evaluating an expression step-by-step.
- Identify the Variables. In the first step, your students need to look for the letters — such as x, y, or a — that are standing in as variables in the expression.
- Determine the Value of Each Variable. Using the provided information for the problem, determine the value for each variable used in the expression. There could be multiple variables used in a single expression!
- Substitute the Values — Once the values of each variable is known, replace the variables in the expression with their corresponding values.
- Complete the Operation(s) — Students then follow the order of operations rules to complete any whole number operations that are represented in the expression until you have simplified the expression down to a single numerical value.
Equivalent Expressions – A How-To Guide
Identifying and generating equivalent expressions is another skill your students will likely come across during their algebraic expressions unit. Equivalent expressions are numerical statements that have the same value, but may look different. An example of two equivalent expressions are 3(8+5x) and 24 + 15x. Even though the expressions look different, they would equal the same number if evaluated with the same value for x.
So, what are some ways to make equivalent expressions? Here's a quick guide for creating expressions with the same value.
1. Use the Distributive Property
The distributive property can be used to create equivalent expressions. This math rule tells us that if you multiply a number by the sum or difference of two other numbers, you will be able to distribute the multiplication to each term within the parentheses. Finally, you can add or subtract the results.
For example, let's say you have the expression 2(x + 9) - 7. If you use the distributive property, you can create the expression 2x + 18 - 7. After subtracting 18 and 7, this simplifies to 2x + 11. These two expressions are equivalent.
2. Combine Like Terms
Another way to create an equivalent expression is to combine terms with the same variables and exponents.
For example, in the expression 6x + 2x, you can combine the "6x" and "2x" terms to get "8x."
3. Combine Constants
Constants are the numbers without variables in the expression. Combining these numbers will create an expression that is the same value as the first.
For example, in the expression 4x + 2 + 3, you can combine "2" and "3" to get "5," resulting in 4x + 5.
- Plus Plan

Distributive Property Match-Up
Use your understanding of the greatest common factor and the distributive property to match equivalent expressions.
- Plus Plan

Emoji Equation Riddles - Determine the Unknown
Build problem-solving and critical thinking skills with printable Emoji Math Riddle task cards.
- Plus Plan

Evaluating Expressions – Paper Chain Activity
Use your understanding of the order of operations to evaluate expressions with one or two variables with this paper chain activity.
- Plus Plan

Writing Numerical Expressions – Google Slides Interactive Activity
Write and solve numerical expressions based on descriptions using a letter for the unknown quantity with this interactive activity.
- Plus Plan
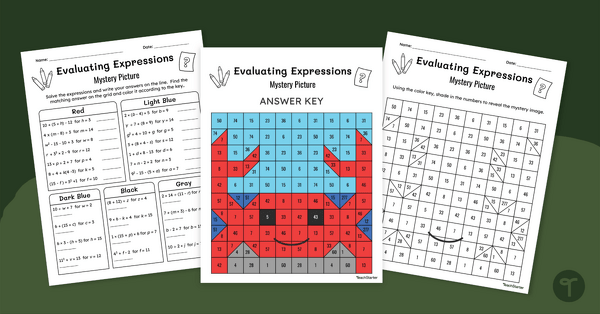
Evaluate Expressions (One Variable) – Mystery Picture Worksheet
Substitute values for variables and use your understanding of the order of operations to solve expressions with this worksheet.
- Plus Plan
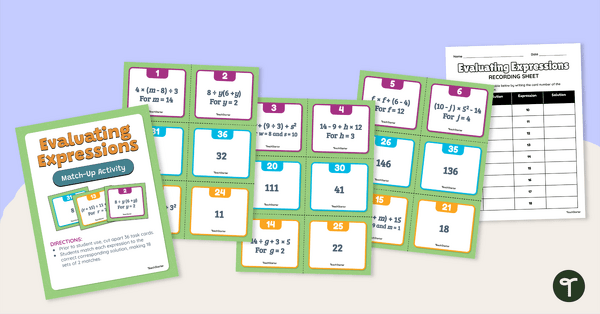
Evaluating Expressions – Match-Up Activity
Practice substituting values for variables while evaluating expressions with this match-up activity designed for 6th-grade students.
- Plus Plan

Algebraic Expressions – Google Slides Interactive Activity
Practice writing, reading, and solving algebraic expressions with this set of interactive activities.
- Plus Plan

Evaluating Expressions – Task Cards
Use this set of 24 task cards to practice evaluating expressions with a single variable.
- Plus Plan

Evaluating Expressions – Worksheet
Challenge your students to evaluate expressions with one or two variables by completing this worksheet.
- Plus Plan

Algebraic Expressions – Task Cards
Read, write, and solve algebraic expressions with this set of 24 task cards.